无损传输线模型

1 介绍

理想传输线模型与约束

理想的传输线模型

连接两点，电压与电流变化瞬时无损传播。
这在现实中是不可能的。

物理约束

信号传播速度不超过光速 $c ≃ 3 \times 10^{8} m / s$ （爱因斯坦相对论）。

为了研究波在真实传输线上的传输规律，我们来对其建模。

2 电报方程(Telegrapher's equations)

无损传输线模型

可视作无限长，无损的双导线系统。
每个微小段长 Δx 对应：
- 电感：LΔx
- 电容：CΔx

如图所示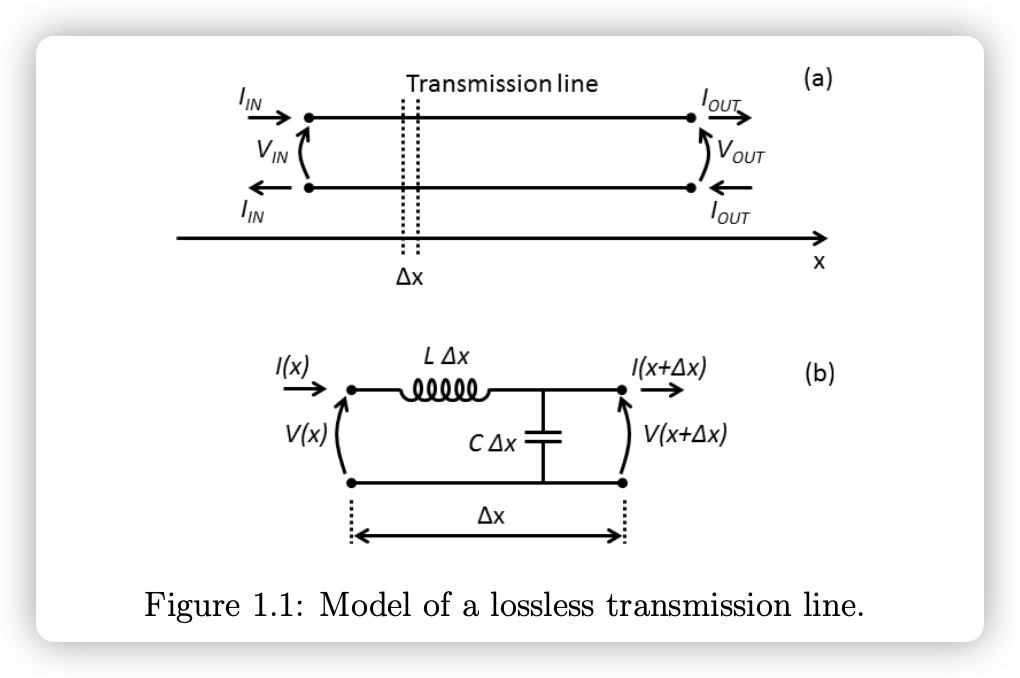：无损传输线模型

将传输线在坐标 $x$ 处到 $x + Δ x$ 这一小段视作电路：串联电感 $L Δ x$ 和并联电容 $C Δ x$

对任意瞬时 $t$ ，在 $x$ 处电压为 $v (x, t)$ ，电流为 $i (x, t)$ 。

根据基尔霍夫电压定律（KVL）与基尔霍夫电流定律（KCL），对小段 $Δ x$ 有:

KVL (电感左端):

V (x, t) = V (x + Δ x, t) + L Δ x \frac{\partial I (x, t)}{\partial t}

整理式子，两边同时除以 $Δ x$ 可得:

\begin{matrix} (1) & \frac{v (x + Δ x, t) - v (x, t)}{Δ x} + L \frac{\partial I (x, t)}{\partial t} = 0 \end{matrix}

KCL (电容右端):

I (x, t) = I (x + Δ x, t) + C Δ x \frac{\partial C (x + Δ x, t)}{\partial t}

整理式子，两边同时除以 $Δ x$ 可得:

\begin{matrix} (2) & \frac{I (x + Δ x, t) - I (x, t)}{Δ x} + C \frac{\partial V (x + Δ x, t)}{\partial t} = 0 \end{matrix}

对公式 1, 2 取极限 $l i m Δ x \to 0$ , 整理可得 Telegrapher’s equations（电报方程）:

\begin{matrix} (3) & \frac{\partial V}{\partial x} + L \frac{\partial I}{\partial t} = 0 \end{matrix}

\begin{matrix} (4) & \frac{\partial I}{\partial x} + C \frac{\partial V}{\partial t} = 0 \end{matrix}

电报方程揭示了无损传输线中的信号传播行为。

3 波动方程

我们已经得到了电报方程，但我们希望更进一步探究波在传输线上的传播规律。

对等式 3 关于 x 求偏导，对公式 4 关于 t 求偏导:

\begin{matrix} (5) & \frac{\partial^{2} v}{\partial x^{2}} = - L \frac{\partial^{2} I}{\partial x \partial t} \end{matrix}

\begin{matrix} (6) & \frac{\partial^{2} I}{\partial x \partial t} = - C \frac{\partial^{2} v}{\partial t^{2}} \end{matrix}

将等式 6 带入等式 5 中可得波动方程 (wave equation):

\begin{matrix} (7) & \frac{\partial^{2} v}{\partial x^{2}} = L C \frac{\partial^{2} v}{\partial t^{2}} \end{matrix}

而波动方程的一般形式为(从物理系统的受力分析推导得出):

\begin{matrix} (8) & \frac{\partial^{2} v}{\partial x^{2}} = v^{2} \frac{\partial^{2} v}{\partial t^{2}} \end{matrix}

对比等式 7 和 8 可以得出，电压、电流沿线传播的速度

\begin{matrix} (9) & v = \frac{1}{\sqrt{L C}} \end{matrix}

信号 $f (x, t)$ 可被拆解为以速度 $v$ 沿 $x$ 方向向前的波和信号 $x$ 方向向后的信号

\begin{matrix} (10) & f (x, t) = f_{+} (x - v t) + f_{-} (x + v t) \end{matrix}

在不失一般性的前提下，我们假设其为正弦波。

为什么假设为正弦波

合理性: 几乎所有信号都可以用正弦波叠加来表示
简化运算: 将计算聚焦在振幅与相位上，不需要处理复杂的波形变化

由公式 9 可得，

\begin{matrix} (11) & λ = \frac{v}{f} = \frac{2 π}{k} \end{matrix}

其中， $w = 2 π f = 2 π \frac{v}{λ}$

验证

f_{+}

与

f_{-}

满足波动方程

对等式 10 进行傅里叶变换, 可得

f_{+} (x, t) = A_{+} e^{- i k x} e^{i w t}

f_{-} (x, t) = A_{-} e^{i k x} e^{i w t}

对 $f_{+}$ 分别关于 $t$ 和 $x$ 求二阶导可得:

\frac{\partial^{2} f_{+}}{\partial^{2} t_{+}} = - w^{2} A_{+} e^{- i k x} e^{i w t} = - w^{2} f_{+}

\frac{\partial^{2} f_{+}}{\partial^{2} x} = - k^{2} A_{+} e^{- i k x} e^{i w t} = - k^{2} f_{+}

代入波动方程 8 中可得:

- w^{2} f_{+} = - v^{2} k^{2} f_{+}

在 $k = \frac{w}{v}$ 条件下满足波动方程(大部分情况下成立)。

$f_{-}$ 同理, 故可得两式均满足波动方程。

例题

Find the wavelength and the propagation speed of a sinusoidal signal at $f = 1 G H z$ in a coaxial cable with a capacitance per unit length $C = 95 p F / m$ , and an inductance per unit length $L = 220 n H / m$ .

Solution

v = \frac{1}{\sqrt{L C}} = \frac{1}{\sqrt{95 \times 10^{- 23} \times 220 \times 10^{- 9}}} ≃ 2.18 \times 10^{8} m / s

λ = v / f ≃ 0.22 m

4 波动理论的应用讨论

为什么在电路中有时必须考虑波动理论（wave theory）

在低频信号（比如 50 Hz）下，信号的波长非常长（约 3000 km），远远大于电路尺寸，所以可以忽略波动效应，用简单的电压/电流分析即可。
但在高频信号（比如 1 GHz）下，波长变得很短（约 15 cm），如果电路连接线的长度接近或超过这个波长，就必须考虑波动效应。

这时，信号在导线中会以波的形式传播，必须用传输线理论（transmission line theory）来分析，比如微带线（microstrip）上的信号传播。

结论

当连接线的长度接近信号波长时，不能再用简单的电路模型，必须考虑波动传播。这就是为什么在高速电路设计中，波动理论变得重要。

为什么波长短时要考虑波动效应

波长短意味着空间变化快波长 𝜆 是波形重复的空间尺度。
当波长很短时，信号在空间上变化得非常快：
一根导线长度如果接近或超过波长，就不能再假设“电压在整条线上是一样的” 不同位置的电压/电流会有相位差，甚至出现 反射、驻波、干涉 这时，必须用波动理论来描述信号传播，而不是简单的电路模型。
判断标准
如果导线长度 $𝐿$ 满足: $L ≳ \frac{λ}{10}$ 就必须考虑波动效应。
比如：
1 GHz 信号，波长约 15 cm → PCB 上的 5 cm 微带线就可能出现反射和失真
50 Hz 信号，波长约 3000 km → 家用电路几米长，完全可以忽略波动效应

5 特性阻抗

在无损传输线中, 由电报方程可知，为支持振荡的电压，必存在振荡的电流。

我们可以进一步的思考: 电压和电流之间是否存在一个恒定的关系，也就是一个特性阻抗 $Z_{0}$ , 使得 $V_{+} (w) = Z_{0} (w) I_{+} (w)$

为继续探究电压与电流的关系，我们可以假设一个正向传播的正弦波:

\begin{matrix} (12) & V = V_{+} e^{- i k x} e^{i w t} \end{matrix}

\begin{matrix} (13) & I = I_{+} e^{- i k x} e^{i w t} \end{matrix}

将电压公式 12 与电流公式 13 分别带入第二电报公式，即公式 4 中可得:

\begin{matrix} (14) & i w C V_{+} e^{- i k x} e^{i w t} = i k I_{+} e^{- i k x} e^{i w t} \end{matrix}

简化并代入 $k = w / v$ 和 $v = 1 / \sqrt{L C}$ 可得

\begin{matrix} (15) & V_{+} = \sqrt{\frac{L}{C}} I_{+} \end{matrix}

可得，电流与电压的关系，即特性阻抗(characteristic impedance) $Z_{0}$ 如下:

\begin{matrix} (16) & Z_{0} = \sqrt{\frac{L}{C}} \end{matrix}

在无损传输线中，特性阻抗是一个实数。

仅用一个复数电压或电流描述正向传播信号

一个沿正向传播的信号可以仅用一个复数电压或电流幅度来描述：

V_{F} (x, t) = V_{+} e^{- i k x} e^{i ω t}

I_{F} (x, t) = I_{+} e^{- i k x} e^{i ω t} = \frac{V_{+}}{Z_{0}} e^{- i k x} e^{i ω t}

类似地，对一个沿反向传播的信号进行相同的推导：

V_{B} (x, t) = V_{-} e^{+ i k x} e^{i ω t}

I_{B} (x, t) = I_{-} e^{+ i k x} e^{i ω t} = \frac{V_{-}}{Z_{0}} e^{+ i k x} e^{i ω t}

请注意在 $V_{-} / Z_{0}$ 中的负号。
这意味着电流“指向”反方向。

我们将会看到，特性阻抗 $Z_{0}$ 在高频电路设计中具有根本性的重要性。
这就是为什么你必须始终知道所用电缆的特性阻抗（通常是 50 Ω）！

同样重要的是要理解，改变传输线的几何结构（这会改变单位长度的电感 $L$ 和电容 $C$ 将会同时改变相速度和特性阻抗。
这正是设计微波电路元件时常用的方法。

无损传输线模型 ​

1 介绍 ​

2 电报方程(Telegrapher's equations) ​

3 波动方程 ​

4 波动理论的应用讨论 ​