有限传输线模型

1 有限传输线的反射

考虑一条无限长的传输线，信号沿正向传输。根据电报方程，电压和电流由特性阻抗 $Z_{0}$ 关联。

1.1 开路

如果在某处切开并开路:

开路处电流必须始终为零。
信号无法继续前进，也不会被吸收（因为没有电阻消耗功率），唯一可能是完全反射。
开路条件下，正向电流与反射电流大小相等、方向相反。

开路信号

1.2 短路

正向电压和反射电压之和为零。
同样发生完全反射，但这次是电压波相互抵消。

1.3 接入阻抗

如果终端接入阻抗 $Z_{L}$ :

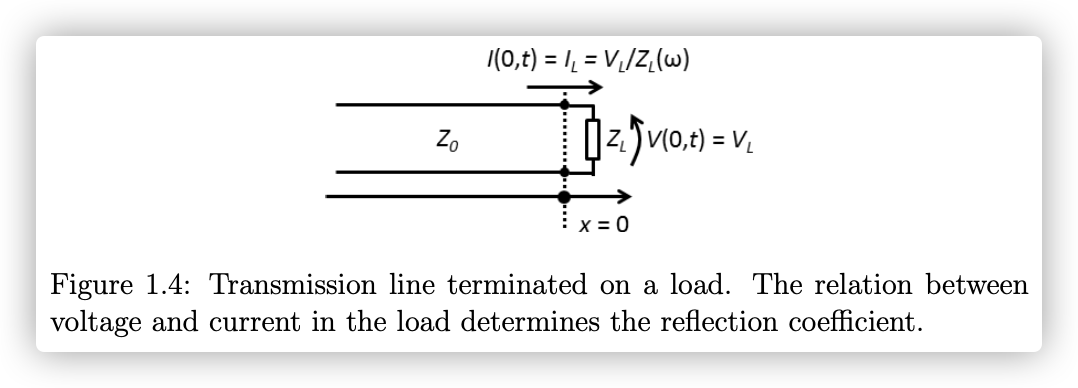
x=0 处的阻抗

部分信号被反射，部分被吸收（在 $Z_{L}$ 的实部上耗散）。

对于正弦波，总体的电压和电流由前向波和反射波共同构成:

\begin{matrix} (1) & V (x, t) = V_{+} e^{- i k x} e^{i w t} + V_{-} e^{i k x} e^{i w t} \end{matrix}

电流可以用阻抗和电压来表示:

\begin{matrix} (2) & I (x, t) = \frac{V_{+}}{Z_{0}} e^{- i k x} e^{i w t} - \frac{V_{-}}{Z_{0}} e^{i k x} e^{i w t} \end{matrix}

电压和电流由正向波与反射波叠加而成。

为什么电压求和，电流求差

电压是标量量（严格说是两点间的电位差），在同一点上，正向波和反射波的电压直接相加。

电压没有方向，是一个可正可负可为 0 的值。

如果有方向，那反向电流用电压写出时的表达式会不同。

在 $x = 0$ 处电压和电流的关系由阻抗 $Z_{L}$ 决定

\begin{matrix} (3) & \frac{V (0, t)}{I (0, t)} = \frac{V_{+} + V_{-}}{V_{+} - V_{-}} Z_{0} = Z_{L} \end{matrix}

该式也揭示了正向波和反射波之间的关系:

\begin{matrix} (4) & V_{-} = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} V_{+} = Γ V_{+} \end{matrix}

$Γ$ 被定义为反射系数，一般为复数，并且模长满足：

0 \leq | Γ | \leq 1

值为 0 意味着没有反射，而 1 则是全反射。

特殊情况： $Z_{L} = Z_{0}$ 时， $Γ = 0$

此时信号完全进入负载，不会反射，实现最大功率传输。

2 阻抗变换 (Impedance transformation)

2.1 等效阻抗的推导

前面我们已经讨论了在电路连接负载阻抗 $Z_{L}$ 的情况，那么现在，我们对负载传输线上某处的等效阻抗进行研究。

在传输线上，距离负载 $d$ 处的等效阻抗 $Z_{e} q$ 如何由负载阻抗 $Z_{L}$ 和特性阻抗 $Z_{0}$ 决定。

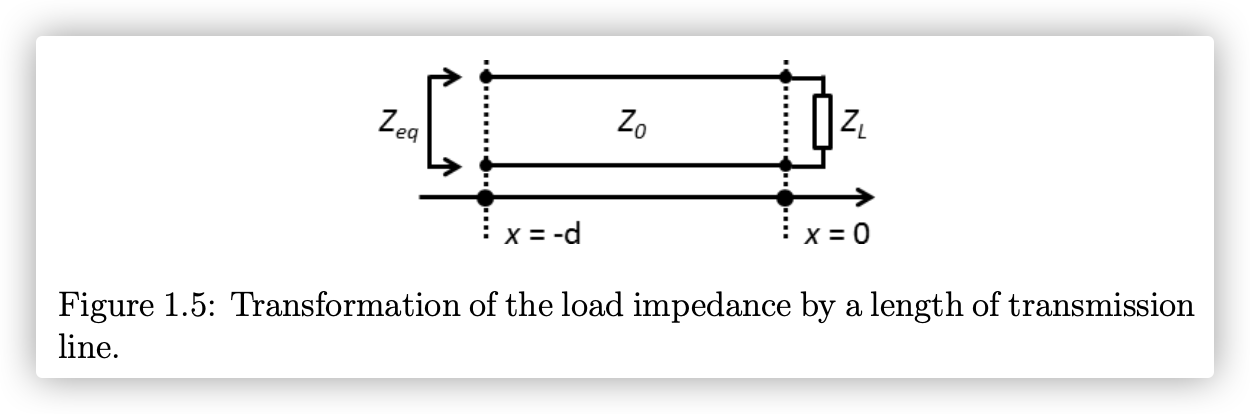
等效阻抗在x=-d处

如图所示负载电阻 $Z_{L}$ 所在位置为 $x = 0$ ，电压与电流在 $x = - d$ 处为

\begin{matrix} (5) & V (- d, t) = V_{+} e^{i k d} e^{i w t} + V_{-} e^{- i k d} e^{i w t} = V_{+} e^{i w t} (e^{i k d} + Γ e^{- i k d}) \end{matrix}

\begin{matrix} (6) & I (- d, t) = I_{+} e^{i k d} e^{i w t} + I_{-} e^{- i k d} e^{i w t} = (\frac{V_{+}}{Z_{0}}) e^{i w t} (e^{i k d} - Γ e^{- i k d}) \end{matrix}

故等效阻抗 $Z_{e} q$ 为

\begin{matrix} (7) & Z_{e} q = \frac{V (- d, t)}{I (- d, t)} = Z_{0} \frac{e^{i k d} + Γ e^{- i k d}}{e^{i k d} - Γ e^{- i k d}} = Z_{0} \frac{1 + Γ e^{- 2 i k d}}{1 - Γ e^{- 2 i k d}} \end{matrix}

将 $Γ = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} V_{+}$ 代入可得

\begin{matrix} (8) & Z_{i n} (d) = Z_{0} \frac{Z_{L} + j Z_{0} \tan k d}{Z_{0} + j Z_{L} \tan k d} \end{matrix}

详细计算过程

代入 $Γ = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} V_{+}$ 后：

Z_{i n} = Z_{0} \cdot \frac{1 + \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} e^{- 2 j k d}}{1 - \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} e^{- 2 j k d}}

分子分母同时乘以 $(Z_{L} + Z_{0})$ ：

Z_{i n} = Z_{0} \cdot \frac{(Z_{L} + Z_{0}) + (Z_{L} - Z_{0}) e^{- 2 j k d}}{(Z_{L} + Z_{0}) - (Z_{L} - Z_{0}) e^{- 2 j k d}}

由欧拉公式 $e^{i x} = c o s x + i s i n x$ 可得

e^{- 2 j k d} = \cos (2 k d) - j \sin (2 k d)

分子（记为 $N$ ）与分母（记为 $D$ ）：

N = (Z_{L} + Z_{0}) + (Z_{L} - Z_{0}) \cos (2 k d) - j (Z_{L} - Z_{0}) \sin (2 k d)

D = (Z_{L} + Z_{0}) - (Z_{L} - Z_{0}) \cos (2 k d) + j (Z_{L} - Z_{0}) \sin (2 k d)

分别代入三角恒等式:

\cos (2 k d) = \frac{1 - \tan^{2} (k d)}{1 + \tan^{2} (k d)}, \sin (2 k d) = \frac{2 \tan (k d)}{1 + \tan^{2} (k d)}

提取公因子可得:

分子：
$N = \frac{(Z_{L} + Z_{0}) (1 + \tan^{2} k d) + (Z_{L} - Z_{0}) (1 - \tan^{2} k d) - j (Z_{L} - Z_{0}) 2 \tan k d}{1 + \tan^{2} k d}$ $= \frac{[2 Z_{L} + 2 Z_{0} \tan^{2} k d] - j [2 (Z_{L} - Z_{0}) \tan k d]}{1 + \tan^{2} k d}$
分母
$D = \frac{(Z_{L} + Z_{0}) (1 + \tan^{2} k d) - (Z_{L} - Z_{0}) (1 - \tan^{2} k d) + j (Z_{L} - Z_{0}) 2 \tan k d}{1 + \tan^{2} k d}$ $= \frac{[2 Z_{0} + 2 Z_{L} \tan^{2} k d] + j [2 (Z_{L} - Z_{0}) \tan k d]}{1 + \tan^{2} k d}$

约去公共分母 $1 + \tan^{2} (k d)$ 与公共因子 $2$ ，得到:

Z_{i n} = Z_{0} \cdot \frac{Z_{L} + Z_{0} \tan^{2} (k d) - j (Z_{L} - Z_{0}) \tan (k d)}{Z_{0} + Z_{L} \tan^{2} (k d) + j (Z_{L} - Z_{0}) \tan (k d)}

展开分子可得:

\begin{aligned} N & = Z_{L} + Z_{0} \tan^{2} (k d) - j (Z_{L} - Z_{0}) \tan (k d) \\ = Z_{L} + Z_{0} \tan^{2} (k d) - j Z_{L} \tan (k d) + j Z_{0} \tan (k d) \\ = (Z_{L} - j Z_{L} \tan (k d)) + (Z_{0} \tan^{2} (k d) + j Z_{0} \tan (k d)) \\ = Z_{L} (1 - j \tan (k d)) + Z_{0} \tan (k d) (\tan (k d) + j) (右 式 提 出 j) \\ = Z_{L} (1 - j \tan (k d)) + j Z_{0} \tan (k d) (1 - j \tan (k d)) \\ = (Z_{L} + j Z_{0} \tan (k d)) (1 - j \tan (k d)) \end{aligned}

对分母展开:

\begin{aligned} D & = Z_{0} + Z_{L} \tan^{2} (k d) + j (Z_{L} - Z_{0}) \tan (k d) \\ = Z_{0} + Z_{L} \tan^{2} (k d) + j Z_{L} \tan (k d) - j Z_{0} \tan (k d) \\ = (Z_{0} - j Z_{0} \tan (k d)) + (Z_{L} \tan^{2} (k d) + j Z_{L} \tan (k d)) \\ = Z_{0} (1 - j \tan (k d)) + Z_{L} \tan (k d) (\tan (k d) + j) \\ = Z_{0} (1 - j \tan (k d)) + j Z_{L} \tan (k d) (1 - j \tan (k d)) \\ = (Z_{0} + j Z_{L} \tan (k d)) (1 - j \tan (k d)) \end{aligned}

因此：

Z_{i n} = Z_{0} \cdot \frac{(Z_{L} + j Z_{0} \tan (k d)) (1 - j \tan (k d))}{(Z_{0} + j Z_{L} \tan (k d)) (1 - j \tan (k d))}

分子分母的 $(1 - j \tan (k d))$ 约去，得到最终形式：

Z_{i n} (d) = Z_{0} \cdot \frac{Z_{L} + j Z_{0} \tan (k d)}{Z_{0} + j Z_{L} \tan (k d)}

若 $Z_{L} = Z_{0}$ ，则 $Γ = 0$ ，整条线上阻抗恒为 $Z_{0}$ 。
阻抗随长度呈周期性变化：
$\begin{matrix} (9) & Z_{e q} (k d) = Z_{e q} (k d + n π), n \in Z \end{matrix}$

例题

An impedance $Z_{L} = 30 + 10 i Ω$ is connected to a 1m transmission line with a propagation velocity $v = 0.6 c$ , and a characteristic impedance $Z_{0} = 50 Ω$ . Find the equivalent impedance at $f = 100 MHz$

计算：

反射系数： $Γ = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} = - 0.23 + 0.15 j$
相位常数： $k = \frac{ω}{v} = \frac{2 π f}{v} = 3.49 rad/m$
等效阻抗： $\begin{aligned} Z_{e q} & = 50 \cdot \frac{1 + Γ e^{- 2 j k d}}{1 - Γ e^{- 2 j k d}} \\ \approx 50 \cdot \frac{1 + (- 0.23 + 0.15 i) e^{- 6.98 i}}{1 - (- 0.23 + 0.15 i) e^{- 6.98 i}} \\ \approx 50 \cdot \frac{1 + (- 0.23 + 0.15 i) (0.77 - 0.64 i)}{1 - (- 0.23 + 0.15 i) (0.77 - 0.64 i)} \\ \approx (37.3 + 21.2 i) Ω \end{aligned}$

2.2 三种特殊情况

根据公式 8 可得对于长度为 $d$ 的传输线，端接负载 $Z_{L}$ ，输入等效阻抗为:

Z_{e q} = Z_{0} \frac{Z_{L} + j Z_{0} \tan (k d)}{Z_{0} + j Z_{L} \tan (k d)}

2.2.1. 短路负载 ( $Z_{L} = 0$ )

推导

代入 $Z_{L} = 0$ :

Z_{e q} = Z_{0} \frac{0 + j Z_{0} \tan (k d)}{Z_{0} + j \cdot 0 \cdot \tan (k d)} = Z_{0} \cdot \frac{j Z_{0} \tan k d}{Z_{0}} = j Z_{0} \tan (k d)

Z_{e q} = j Z_{0} \tan (k d)

结论:

→ 若 $Z_{0}$ 为实数，则 $Z_{e q}$ 始终为纯虚数（纯电抗），随长度周期性变化。

2.2.2 开路负载 ( $Z_{L} = \infty$ )

推导

代入 $Z_{L} \to \infty$ ，分子分母同时除以 $Z_{L}$ ：

Z_{eq} = Z_{0} \cdot \frac{1 + j \frac{Z_{0}}{Z_{L}} \tan (k d)}{\frac{Z_{0}}{Z_{L}} + j \tan (k d)}

当 $Z_{L} \to \infty$ ，有 $\frac{Z_{0}}{Z_{L}} \to 0$ ，于是：

Z_{eq} = Z_{0} \cdot \frac{1}{j \tan (k d)} = - j Z_{0} \cot (k d)

Z_{e q} = - j Z_{0} \cot (k d) = - j Z_{0} \tan (k d - π / 2)

结论:

→ 若 $Z_{0}$ 为实数，则 $Z_{e q}$ 始终为纯虚数（纯电抗）

→ 注意当 $k d = \frac{π}{2} + n π$ (n 是正整数)时，开路会被转换成短路。

2.2.3 匹配负载（ $Z_{L} = Z_{0}$ ）：

Z_{e q} = Z_{0} \cdot \frac{Z_{0} + j Z_{0} \tan (k d)}{Z_{0} + j Z_{0} \tan (k d)} = Z_{0}

结论:

匹配时输入阻抗恒等于 $Z_{0}$ ，与传输线长度无关。

2.2.4. 四分之一波长线

条件： $d = λ / 4$ 且 $Z_{L}$ 为实数，其中

λ = \frac{2 π}{k}, k d = \frac{π}{2}

结果：

Z_{e q} = Z_{0} \frac{Z_{L} + j Z_{0} \tan (k d)}{Z_{0} + j Z_{L} \tan (k d)} = Z_{0} \frac{Z_{L} + j Z_{0} \tan (π / 2)}{Z_{0} + j Z_{L} \tan (π / 2)} = \frac{Z_{0}^{2}}{Z_{L}}

性质： 当 $Z_{0}$ 与 $Z_{L}$ 为实数时， $Z_{e q}$ 为实数；且当 $Z_{L}$ 增大时， $Z_{e q}$ 减小。

2.3 四分之一波长变换器

当 $d = λ / 4$ ，即 $k d = π / 2$ ：

Z_{e q} = j Z_{0} \tan (π / 2) = \infty

结论: → 短路变开路，开路变短路。

3 阻抗匹配

阻抗匹配的意义

在电路和传输线中，源和负载之间的阻抗关系决定了能量传输的效率。

最大功率传输定理：由本章1.3节可知当负载阻抗 $Z_{L} = Z_{S}$ 时，源到负载的功率传输最大。
阻抗匹配不仅影响功率传输，还影响放大器噪声优化、天线设计、滤波器级联等。
在实际中，负载往往是变化的或复杂的，常常需要通过电路结构（变压器、调谐器等）将负载阻抗变换为更合适的值。
阻抗匹配通常用匹配网络完成，而匹配网络一般被设计在窄频段中运行，更宽的频段也存在，但不在本节讨论的范围。

3.1 $λ / 4$ 变压器（Quarter-wave transformer）

原理：在源与负载之间插入一段长度为 $λ / 4$ 的传输线。
输入阻抗变换公式：
$Z_{i n} = \frac{Z_{0}^{2}}{Z_{L}}$
匹配条件：
$Z_{0} = \sqrt{Z_{s} Z_{L}}$
局限性：只适用于实数阻抗，对复数负载不能完美匹配。
实际应用中可用多段传输线扩展带宽。

3.2 单支路调谐器（Single-stub tuner）

为解决 $λ / 4$ 变压器只能用于实数阻抗(只有电阻，没有电抗) 的问题，我们尝试使用传输线。

由 2.2可知，终止在开路或短路的传输线，可通过调节其长度，制造任意值的等效阻抗。
利用一段开路或短路的传输线（stub）来补偿负载的虚部（电抗）。
故通过调节 stub 的长度和位置，可以实现阻抗匹配。

数学上常用导纳形式：

Y_{i n} = Y_{1} \frac{Y_{L} + i Y_{1} \tan (β l)}{Y_{1} + i Y_{L} \tan (β l)}

匹配条件：

Y_{i n} = Y_{0} \Rightarrow Γ = 0

在单支路调谐器（single-stub tuner）中，会利用这样一个特性：

负载阻抗通常包含实部（电阻）和虚部（电抗）。
调谐的策略是先用一小段传输线（称为 stub），它的一端接短路或开路，使它本身表现为一个纯电抗元件。
通过合适选择 stub 的长度，就能让它的电抗正好抵消掉负载阻抗中的虚部。
这样一来，剩下的就是纯实数阻抗，再用例如 λ/4 变压器这样的手段，就可以把它匹配到传输线或信号源的阻抗。

一些补充

在传输线上，负载阻抗一般可以写成：

Z_{L} = R + j X

其中

$𝑅$ 是实部（电阻），代表能量消耗或吸收。

$j X$ 是虚部（电抗），代表能量在电场和磁场之间来回震荡，但并不真正消耗。

如果负载有电抗，对理想传输线来说，源 $Z_{0}$ 是纯实数，无法实现最大功率吸收，所以需要另一根传输线来抵消。

以下是两个实例用于学习

3.2.1 例一

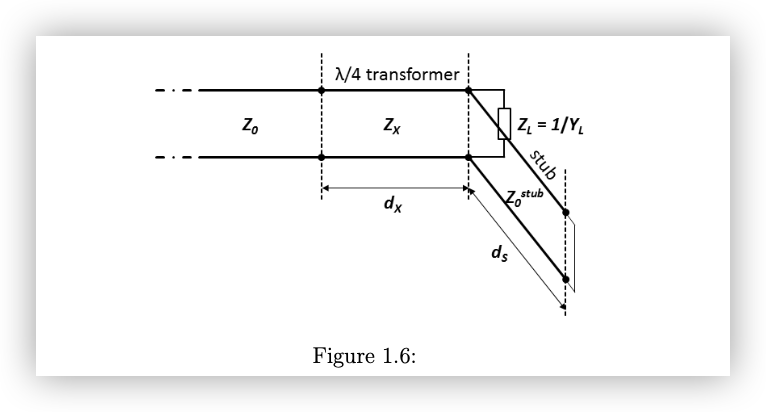
如图所示:

传输线特性阻抗： $Z_{0}$
负载导纳：
$Y_{L} = G_{L} + i B_{L}$
其中：
- $G_{L}$ ：电导（实部）
- $B_{L}$ ：电纳虚部（容性或感性）

目标：通过在传输线上并联一个短路 stub，使得总导纳为纯实数，从而实现阻抗匹配。

由 2.2 可知短路 stub 的输入阻抗为：

Z_{i n} = i Z_{s t u b} \tan (k_{s t u b} d_{s t u b})

对应的输入导纳为：

Y_{i n} = \frac{1}{Z_{i n}} = \frac{- i}{Z_{s t u b} \tan (k_{s t u b} d_{s t u b})}

教材中采用归一化形式，写作 (以 $Z_{0}$ 为基准)：

i B_{S} = \frac{1}{Z_{i n}} = \frac{- i}{Z_{0}^{stub} \tan (k_{s t u b} d_{s t u b})}

而负载阻抗的虚部应该与 stub 的虚部相抵消，故

B_{s} = - B_{L} = \frac{- 1}{Z_{0}^{stub} \tan (k_{s t u b} d_{s t u b})}

因此，为了和 $B_{L}$ 抵消，需要的长度 $d_{s}$ 为:

d_{s t u b} = \frac{1}{k_{s t u b}} \arctan \frac{1}{Z_{0}^{stub} B_{L}}

例题

Problem

Match a load impedance $Z_{L} = (70 + 100 j) Ω$ to a $Z_{0} = 500 Ω$ transmission line at frequency $f = 700 MHz$ , using the stub tuner shown in Fig. 1.6.
The characteristic impedance of the stub is $Z_{0}^{stub} = Z_{0} = 500 Ω$ and the phase velocity $v = 0.6 c$ .
Determine the stub length and the distance of the $λ / 4$ transformer.

Solution

From the load admittance we get:

Y_{L} = \frac{1}{Z_{L}} = (4.70 - 6.71 j) mS

From the load susceptance $B_{L} = - 6.71 mS$ , we can calculate the required stub length $d_{S}$ :

d_{S} = \frac{1}{k_{S}} \arctan (\frac{1}{Z_{0} B_{L}}) = \frac{v}{2 π f} \arctan (\frac{1}{Z_{0} B_{L}})

Since $\arctan (x) \approx x$ for small $x$ , this simplifies to:

d_{S} \approx \frac{1}{Z_{0} B_{L}}

Numerically:

d_{S} ≃ 0.0408 m/rad \times (- 1.247) rad

This gives a negative stub length.
This is not really an issue: stub length is typically prescribed in $k d$ with period $π$ .
So we can write:

d_{S} ≃ 0.0408 m/rad \times (- π + 1.247) rad = 77.4 mm

Now we can match the real conductance to the $500 Ω$ transmission line with a $λ / 4$ transformer:

Z_{t r} = \sqrt{\frac{Z_{0}}{G_{L}}} = 324 Ω

This gives us a function of the frequency (see Fig. 1.7), verifying that our design is correct.

3.2.2 例二

有些情况下无法使用不同特性阻抗的传输线，例如在使用同轴电缆时。这时可以采用一种替代的支线调谐器（stub tuner），它只使用具有相同特性阻抗的传输线，如图所示。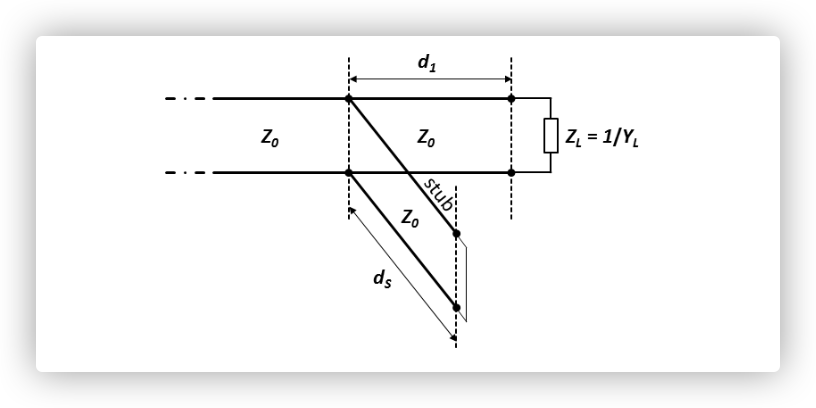结构: 主传输线上在距负载 $d_{1}$ 处接入一段开路 (stub), 长度为 $d_{2}$ ，其特性阻抗同样为 $Z_{0}$ 。

传输线到负载的等效导纳在距离负载 $d_{1}$ 处，等效导纳为

Y_{1} = \frac{1}{Z_{0}} \cdot \frac{1 - Γ e^{- j 2 k d_{1}}}{1 + Γ e^{- j 2 k d_{1}}}

stub 的导纳开路 stub 的输入导纳为

Y_{s} = \frac{j}{Z_{0}} \tan (k d_{2})

匹配条件: 总导纳等于主线的特性导纳

Y_{1} + Y_{s} = Y_{0} = \frac{1}{Z_{0}}

其中 $Y_{s}$ 为纯虚数，而 $Y_{0}$ 是实数, 先由实部条件确定 $d_{1}$ ，再用虚部抵消由 $d_{2}$ 确定。最终得到：

\cos (2 k d_{1} - φ) = \frac{1 - Γ^{2}}{2 Γ}

\tan (k d_{2}) = - \frac{Γ \sin (2 k d_{1} - φ)}{1 + Γ^{2} - 2 Γ \cos (2 k d_{1} - φ)}

例题

题目同 3.2.1。 数值解（示例）： $Z_{0} = 50 Ω$ ，得到 $d_{1} = 60.6 mm$ ， $d_{2} = 21.5 mm$ 。

i k V_{+} = Z (w) I_{+}

有限传输线模型 ​

1 有限传输线的反射 ​

1.1 开路 ​

1.2 短路 ​

1.3 接入阻抗 ​

2 阻抗变换 (Impedance transformation) ​

2.1 等效阻抗的推导 ​

2.2 三种特殊情况 ​

2.2.1. 短路负载 (ZL=0) ​

2.2.2 开路负载 (ZL=∞) ​

2.2.3 匹配负载（ZL=Z0）： ​

2.2.4. 四分之一波长线 ​

2.3 四分之一波长变换器 ​

3 阻抗匹配 ​

3.1 λ/4 变压器（Quarter-wave transformer） ​

3.2 单支路调谐器（Single-stub tuner） ​

3.2.1 例一 ​

3.2.2 例二 ​